Table of contents > Conditional execution (branching) in Nodezator
Nodezator still has a long way to go before fully supporting conditional execution/branching, but much can already be done regarding this with its current features/design. In this chapter we'll explore different ways in which conditional execution can be achieved and what's missing for it to be fully achievable.
Let's jump straight into action by analyzing how a real problem requiring conditional execution can be solved with Nodezator.
Suppose we have data representing a 3D box model and want the model to be changed depending on the requested kind of lid (hinged, sawn or sliding). To keep the problem as fundamental/representative as possible, let's reduce the possibilities to 02 options: either "hinged" or "no lid" (the box without a lid could be used as a prop, for instance). Once we solve the problem, we can then extend our solution to include more options as needed.
The image below depicts a dummy node that returns data representing a box. At this point we still didn't decide whether the box will have lids or not, the node just returns general data describing a box.
The image below depicts 02 different dummy nodes that represent operations that result in the simplified possibilities: a box with a hinged lid or the same initial box with no lid added to it. As you can see, they take exactly one input and return a single value.
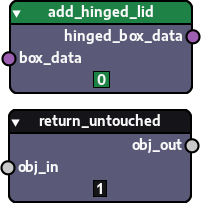
The add_hinged_lid node takes the box data and returns the box data changed to include data describing the hinged lid. The return_untouched node doesn't change the input at all, returning it exactly as it is. That is, the same object that goes in, goes out as well. In mathematics, this kind of function is called an identity function. It is a node I want to add as an app-defined node to Nodezator, that is, one that is available by default (it would probably be added in the "Encapsulations" menu).
Finally, the image below shows a viable solution to our branching problem.
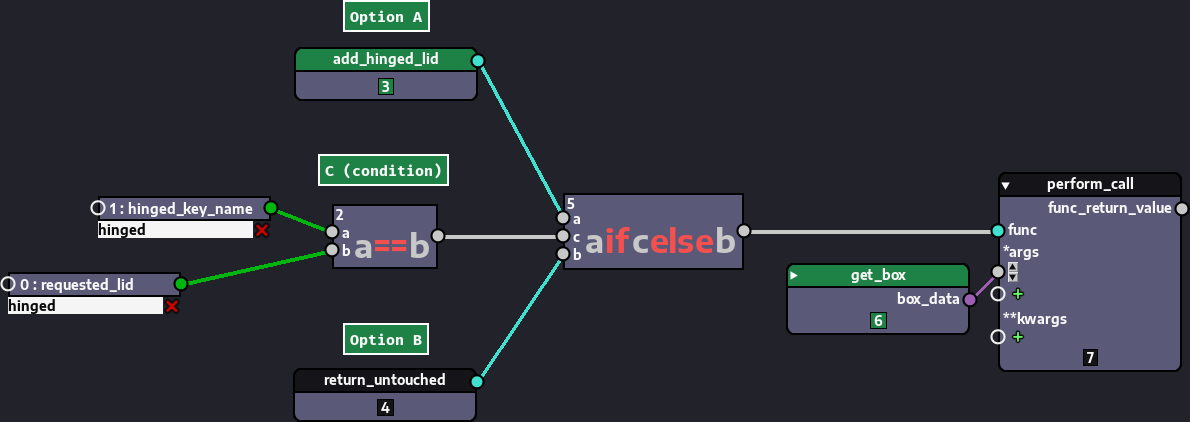
At the center of our solution is the a if c else b operator node. It just represents a conditional expression or ternary operator in Python (it is also called an "inline if-else statement" and other similar names). a and b represent the alternatives and c represents a condition. So, in plain English, what the operation represents is clear: use a if condition is true, else use b.
Everything to the left of the a if c else b node represents the alternatives and condition being passed to the node. The leftmost node, the requested_lid variable just holds a string representing the kind of node that is requested. Then, this requested_lid variable is compared to the hinged_name variable using equality (the a==b node) and the result is fed to the c parameter of the a if c else b node.
If the requested lid equals 'hinged', then a is used, that is, the add_hinged_lid node in callable mode, that is, a reference to the callable that receives the box data and returns the changed data describing a box with a hinged lid. If otherwise, the requested lid is different, than b is used, that is, the return_untouched node in callable mode, which receives the box data and returns it untouched.
The output of a if c else b is then passed to the perform_call node (you can found it in the "Encapsulations" submenu of the popup menu) as the argument for its func parameter. The perform_call node just performs a call with the given callable object and additional arguments given to it and returns the return-value of the call. The perform_call node also takes the box_data output from our get_box node as an argument. In other words, whichever callable comes from the a if c else b node will be called with the box data as an argument and will then return either the box data describing a box with a hinged lid or our original box.
This solved problem represents the most atomic/fundamental/basic problem in conditional execution/branching: choosing between an option or doing nothing.
In text-based Python programming this would often appear in a script as a single if-block without an else-block accompanying it. Something like this:
box_data = get_box(...)
if requested_lid == 'hinged':
box_data = add_hinged_lid(box_data)The exported Python code from our solution will instead represent a text-based script using FP. The code below is a simplified representation of how the graph from our solution would be exported as Python code:
chosen_func = add_hinged_lid if requested_lid == 'hinged' else return_untouched
box_data = get_box()
box_data = perform_call(chosen_func, box_data)Despite the fact that within a node-based interface like Nodezator the a if c else b node doesn't short-circuit because the alternatives must be evaluated before being passed to the node, the solution still doesn't waste any resources. This is so for 02 reasons:
perform_call node and only then the callable is executed.In other words, our solution is efficient.
Now let's extend this problem to work with an additional option: a box with a sawn lid. The image below depicts the solution:
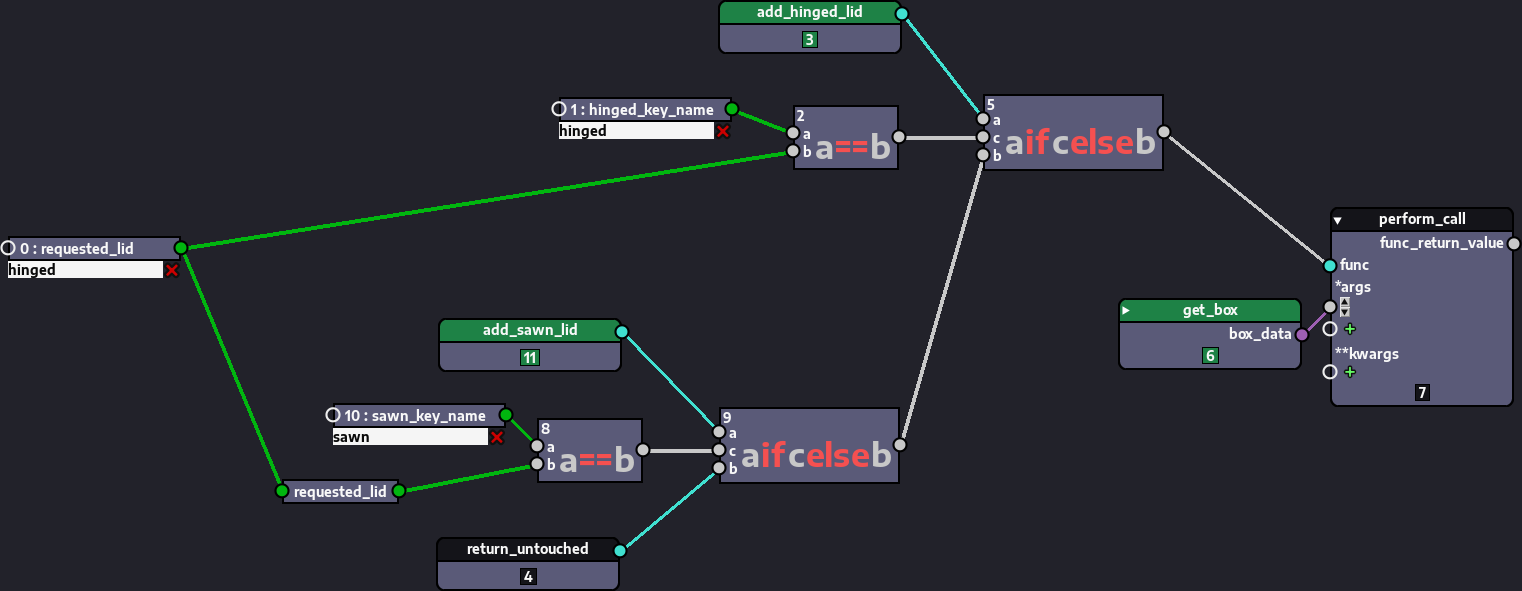
The solution above shows how versatile the ternary operator (the a if c else b node) is.
In this solution, the first ternary operator (the one closer to the center, in the bottom half of the image) executes and, if the requested lid was a sawed-off one, it passes a reference to the add_sawn_lid callable to the next ternary operator. Otherwise, it passes a reference to our identify function, the return_untouched node.
The next ternary operator checks whether the requested lid is a hinged one and, if it is, it passes a reference to add_hinged_lid to the perform_call node. Otherwise, whichever reference is received in its b parameter is passed on, that is, either add_sawn_lid or return_untouched. The call is then performed in the perform_call node with the box data from the get_box node.
Just as shown in the image, this solution can be extended indefinitely, regardless of how much alternatives there are. We just need to chain as much ternary operators as needed.
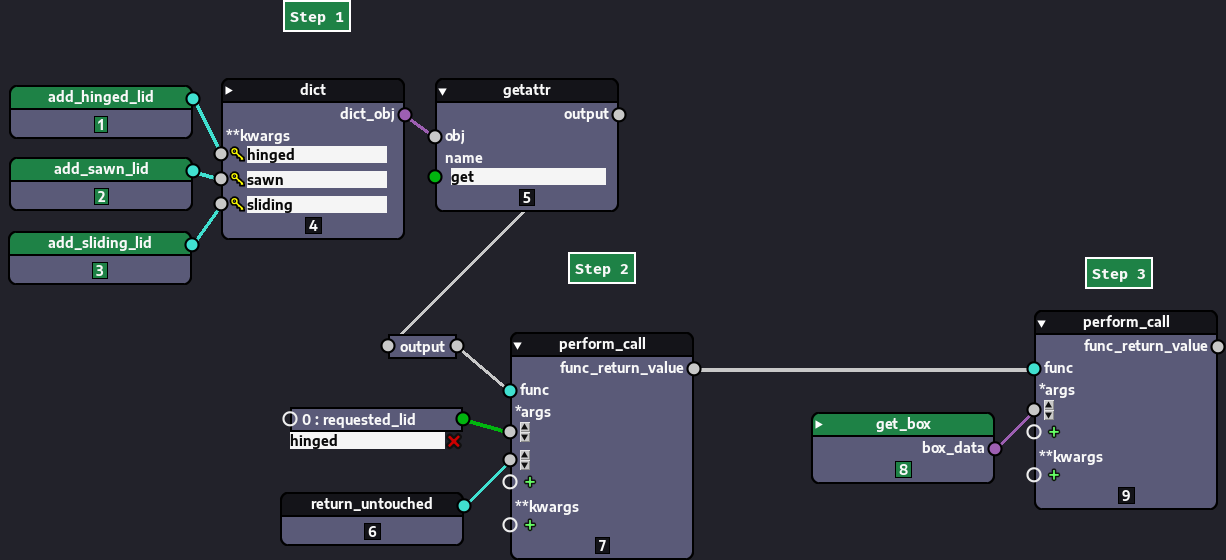
Our solution can still be further simplified in some cases. Whenever the conditions to be evaluated are simple values that correspond to specific options, such different values and respective options can be stored in a dictionary, like demonstrated in the image below:
| Step | Description |
|---|---|
| Build a dict and retrieve its .get() method | |
| Execute the .get() method with the requested_lid, using return_untouched() as a value to be returned in case requested_lid isn't found in the dictionary | |
| Finally, execute the received callable with the box data from get_box() |
As seen in the image, the dict is populated with our options, using the respective lid type name. We then retrieve it's .get() method and call it with the perform_call node, passing the name of our requested lid to it and our identify function return_untouched. If the name of the requested lid corresponds to one of the alternatives stored in the dict (the callable objects), it is returned, otherwise return_untouched is returned instead. Finally, the returned callable is executed in the next perform_call node with our box_data.
This solution is actually not innovative. It works similarly to match/case statements and in fact people have been using it in Python before match/case was implemented and some (maybe many) still use it instead.
There is one case that our solution still needs to address. What if...
In the problems we just explored, the alternatives had the same signature and we only wanted to pass our box_data to them. That is, both our return_untouched identity function and the other alternatives like add_hinged_lid, etc., all accepted a single argument.
However, what if each of the callables required different arguments or we just wanted to pass different arguments to them of our own volition?
The answer is actually simple: we would only need to pass each reference of the callables through a partial node along with the additional arguments. Such node is a representation of the standard library's functools.partial() function. The partial node can be found in the popup menua mong the standard library nodes.
This way we could feed the required/desired arguments to the callables even before the chosen one reaches the perform_call node.
As an example, let's pretend our add_sliding_lid accepts an optional lid_color parameter and we wanted our call to add_sliding_lid (in case it is the requested lid), to include such an argument for the lid_color parameter. All we'd have to do is to pass the reference to our add_sliding_lid callable through the partial node along with the lid_color argument, as demonstrated in the image below:
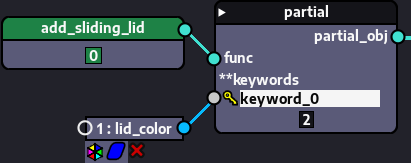
The resulting partial_obj returned by the partial node would then be passed to the ternary operator as usual and, if it were to reach the perform_call node, where it would receive the box_data argument, it would be properly executed with both the box_data and lid_color arguments.
Alternatively, if the order of the arguments was important, we could feed both the box_data and lid_color arguments to the partial node as well. In this case, we'd also need to add partial nodes to the other alternatives and also feed the box_data to them. Also, since we'd be feeding the box_data argument to all alternatives from the very beginning, we wouldn't need to pass the box_data to the perform_call node at the end.
This ability to work with alternatives that have different signatures is actually crucial, because it allow us not only to use alternatives that require different sets of data, but also alternatives that require no data at all.
Our solution so far has been addressing a problem with similar alternatives, that is, different kinds of lids (or no lid at all). All of them require some data to be passed to the chosen alternative. Even in the alternative where no lid is added, the identity function used receives the box_data. However, there are also cases when no data is passed on at all. For instance, if no lid is required, you might instead want to do something completely unrelated, like sending an email or creating an entirely new 3D model. In such cases, we'll be ignoring the existence of the box data entirely. Here's the resulting graph:
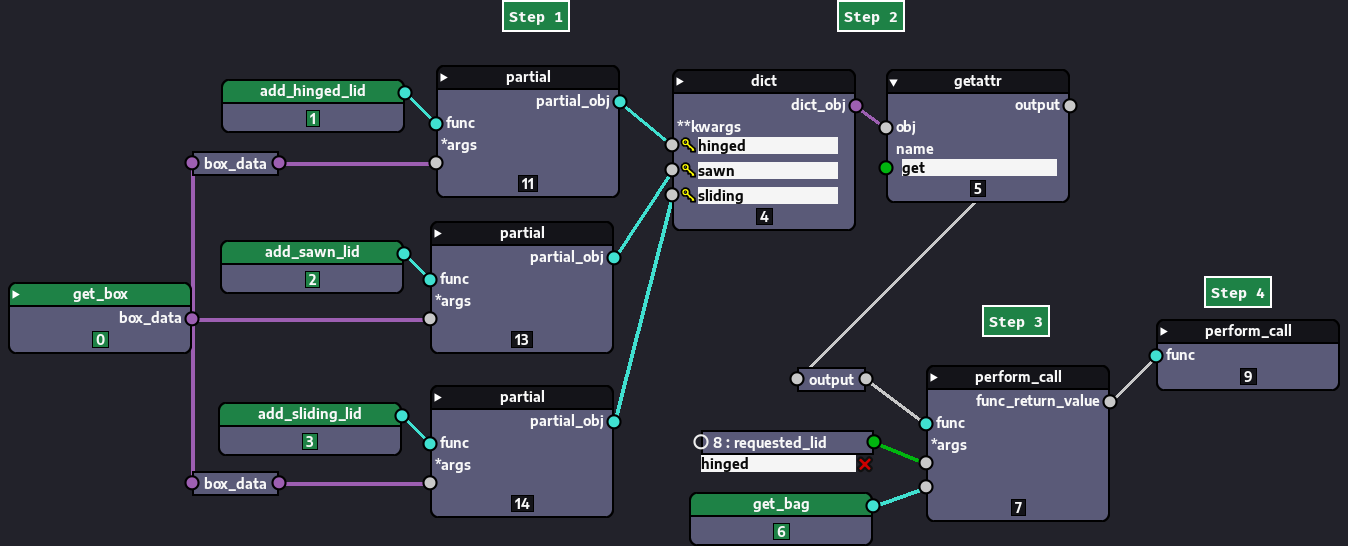
In other words, the get_bag alternative doesn't care about the box data. Also notice that any additional argument needed was fed to the alternative beforehand when turning them into partial objects. All of what we demonstrated guarantees that the alternatives, though sometimes similar to each other, can also represent completely different operations/paths of execution.
Note that the steps are almost the same as in the graph shown in a previous image (the one where we presented the dict-based approach). The main difference is that in the step where we build the dict, we create partial objects before feeding them to the dictionary. In step 03 where we use the perform_call to execute dict.get(), we pass a reference to the callable of the get_bag() node to be returned in case a requested key is not in the dictionary. Whichever callable is returned by dict.get() in step 03, is executed in step 04 by yet another instance of the perform_call node.
There's still a final crucial missing piece for the completion of our solution: subgraphs (group nodes).
Subgraphs are actually an integral part of the solution. Notice that the nodes representing the different alternatives (add_hinged_lid, add_sawn_lid, etc.) we presented in the explored problems are only dummy nodes that represent an atomic operation: adding a lid to a node (or other atomic operation). However, in practice, each different alternative/branch from which we'll be choosing can't always be represented by a single node.
In fact, it often won't, which is precisely why we use a node-based interface to program, so we can combine different nodes to achieve a certain result. For instance, the alternative to create a 3D bag instead would probably be followed by other operations related to that alternative. As such, we'd probably use multiple nodes, not only the one to just create the bag. The options where a lid is added and we keep using the box data, would, in practice, maybe require many nodes to be combined and executed in order to add such lid to our box.
That's where subgraphs (like group nodes in Blender3D) are useful. This is something that will still take a while to land on Nodezator, but is something indispensable in order to be able to fully tap into conditional execution/branching in Nodezator (and also looping).
Once subgraphs/group nodes are implemented, whenever we need to represent a branch/option/alternative that requires the usage of multiple nodes, all we'll have to do is create the nodes, group them together, select which inputs and outputs we want to expose, and use the resulting group node as demonstrated in our solutions: in callable mode, and with help of ternary operators or dictionaries (and partial nodes, to provide dedicated arguments).
match/case and/or if/elif/else nodes would be useful additions, but they are not as urgent, because the ternary operator and the dictionaries can help us already while we implement other more urgent features first. The ternary operator, in particular, being just an application of an if/else clause, can already solve any conditional execution use-case, regardless of the complexity, by being chained. However, match/case and/or if/elif/else nodes could be really useful to simplify part of these use-cases in a way that ternary operators and dictionaries could not.
However, they will probably land in Nodezator only after subgraphs are implemented, since subgraphs are a more crucial and urgent tool to enable the full power of conditional execution/branching.